まず実験
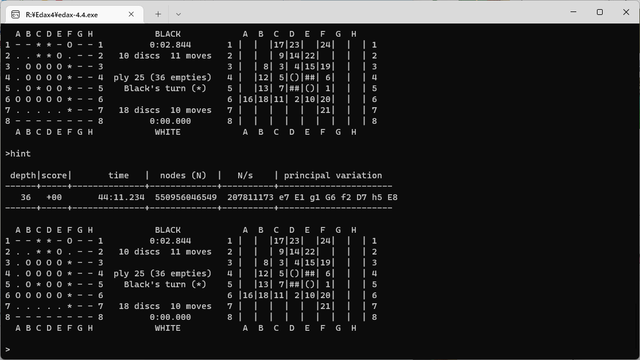
特定の棋譜で、Edax 4.4での26~36個空きの完全読みに必要な時間を計測してみる。
使用するPCのCPUはcore i5-10400(6コア12スレッド、4GHz動作)
棋譜1:f5d6c3d3c4f4c5b3c2e6c6b4b5d2e3a6c1b6f3f6f7e2d1f1e7e1g1g6f2d7d8c7c8g4g3h3g5b7h6h5a4a5a8b2a7g8f8b1a1g2h1g7h8h7h4h2a2a3b8e8
empties: nodes(N) time(sec)
2:18 0
4:154 0
6:974 0
8:4,642 0
10:38,120 0
12:19,338 0
14:126,645 0
16:230,642 0
18:648,803 0
20:3,016,490 0.047
22:19,810,876 0.125
24:88,627,952 0.485
26:315,699,264 1.531
28:949,928,972 4.563
30:7,476,925,380 38.031
32:58,519,816,973 267.531
34:97,436,379,914 455.688
36:550,956,046,549 2651.234
対数グラフにしてみます。
empties(空きマスの数)と、nodes(N)(edaxが読んだ局面の数っぽい数字)
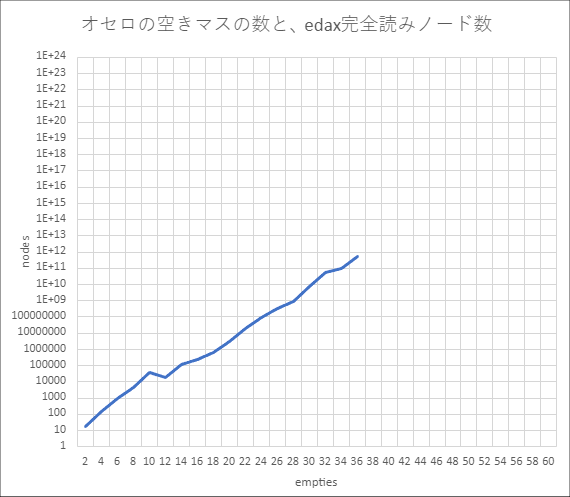
大体直線になってますね。
見ていて思ったのですが、
同じedax 4.4で60個空きの完全読みをしたら、30個空きのときの2乗くらいのnodes(N)になりはしないだろうか?
(というか、60個空きでもnodes(N)は10^20くらいで済むのでは?と思った)
30個空きのときの2乗説で計算してみると、
30個空きのときに
7,476,925,380 nodes(7.477×10^9 nodes)
38.031 secで、
196,600,809 nodes/s(1.966×10^8 nodes/s)
じゃあ、60個空きなら・・・
N = 5.590×10^19 nodes(予想)
60個空きでもnodes/sが同じくらいなら、
N / 1.966×10^8 = 2.844 × 10^11 sec
これは、329.1万日、9011年くらいかかる計算になります。
最序盤の方が最終盤より選択肢が多いことを考えると、1~2桁くらい多い可能性もあるのかなぁ。
それだと、最大90万年くらい。
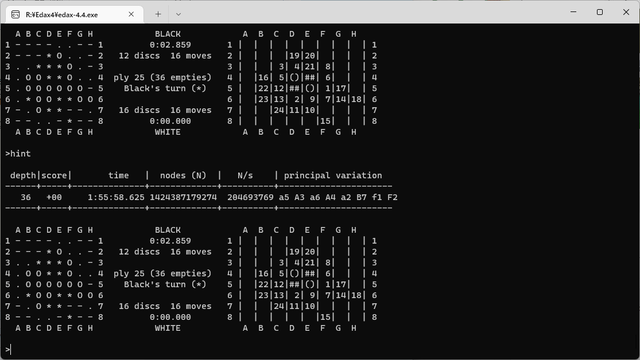
棋譜2:f5d6c3d3c4f4f6f3e6e7d7c5c6g6f8b4g5h6d2e2e3b5b6c7a3a4a5c8h5h4f7g4b3e8f1c2b7a8b8a7a6c1e1d1b1b2a1a2g3h3f2g8d8g1h8g2h7g7h2h1
empties: nodes(N) time(sec)
2:12 0
4:133 0
6:723 0
8:1,229 0
10:9,306 0
12:14,904 0
14:42,245 0
16:92,579 0
18:1,168,654 0.016
20:2,634,411 0.047
22:10,313,490 0.094
24:70,539,971 0.390
26:384,523,477 1.750
28:1,494,098,638 6.609
30:6,588,604,870 35.562
32:29,491,089,280 152.875
34:255,415,796,011 1226.219
36:1,424,387,179,274 6958.625
さっきのグラフに、棋譜2のデータを追加してみます。
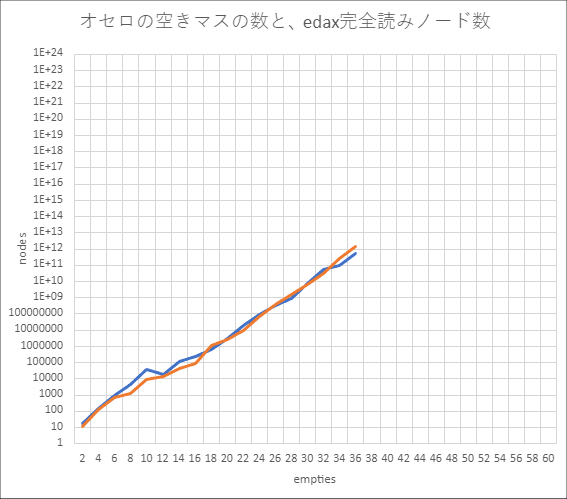
あまり変わらないかな。何十通りもやれば説得力が上がりそうです。
そして、さっきと同じように計算すると、
30個空きのときに
6,588,604,870 nodes(6.588×10^9 nodes)
35.562 secで、
192,909,824 nodes/s(1.929×10^8 nodes/s)
60個空きなら・・・
N = 4.341×10^19 nodes(予想)
N / 1.929×10^8 = 2.250 × 10^11 sec
260.4万日、7131年
うーん、大体1万年以内には終わりそうで、かかっても10万年~100万年くらいかなぁ?
ただし、これは
core i5-10400(6コア12スレッド、4GHz動作)
で1万年以内ということで、最新CPUでは4倍くらい速そうなので・・・
Intel Core i9-13900K vs Intel Core i5-10400
Geekbench 5, 64bit (Multi-Core)
Core i5-10400 5870
Core i9-13900K 23982
core i5-10400で1万年かかる作業は、Core i9-13900Kで2500年くらいで終わると思います。
100万年なら25万年。
つまり、家庭用PC1台ではまだ無理。全然無理。
じゃあ、スパコンだったら?
スパコンて家庭用PCの何倍速いんだろう?
オークリッジ国立研究所のスパコン「Frontier」が1EFLOPS超で1位に─TOP500の2022年6月版が公開
https://it.impress.co.jp/articles/-/23242(2022年5月30日(月))
スパコン「Frontier」:1.102EFLOPS(=1102.00PFLOPS〈ペタフロップス〉、毎秒110京2000兆回)
うちのPCのcore i5-10400は400GFLPOSくらいらしいので・・・ペタの3桁下がテラ(T)、さらに3桁下がギガ(G)なので、単位をGFLOPSに合わせて計算すると、
スパコン「Frontier」:1,102,000,000 GFLOPS
1,102,000,000÷400=2,755,000
え?今の世界最速のスパコンて、うちのPCの275万倍も速いの!?
じゃあ、うちのPCで1万年かかる作業は、32時間で終わるじゃん。
100万年としても3200時間(133日)。
ということで、もう技術的にはオセロの60手(59手)完全読みはできるかも知れません。
『莫大な費用がかかると思うけど、人類の叡智・技術を結集すれば、そろそろかもね』くらいのニュアンス。
※1.102EFLOPSが、オセロの完全読みに使えるのか、そのままの効果が出るのか、という疑問はある。
やるなら、縦取り(F5D6)、斜め取り(F5F6)、並び取り(F5F4)を分けて3通りやって欲しいです。縦取りと斜め取りは引き分け、並び取りは白勝ちになると予想します。
※完全読みと完全解析は私の頭の中では意味が違います。完全読みは最善手か最善手順を1通り示せば良いけど、完全解析は、発生し得る全ての局面の完全読み評価値がDBに入ってる状態だと思っています。将来的には、序盤20手くらいがDBに入ってて終盤40手完全読みが一瞬で終わる状態を作れれば、それもほぼ完全解析とみなせるかな(実用としては60手全部入ってるのと変わらなくなるから)。


